Regola di Ruffini

Se nella divisione fra due polinomi $A(x):B(x)$ il divisore $B(x) = x - a$ con $a \in \mathbb{R}$, si può calcolare velocemente la divisione con resto usando solo i coefficienti numerici tramite la cosiddetta regola di Ruffini.
Per spiegare questa regola utilizzerò come esempio i polinomi:
$$A(x) = x^4 + x^3 + 3x^2 - 5$$

$$B(x) = x - 1$$

1. Si crea una tabella di questo tipo; i coefficienti di $A(x)$ vanno scritti in ordine decrescente di grado; se il termine di un certo grado non è presente nel polinomio, il suo coefficiente è zero e va scritto:
   
   
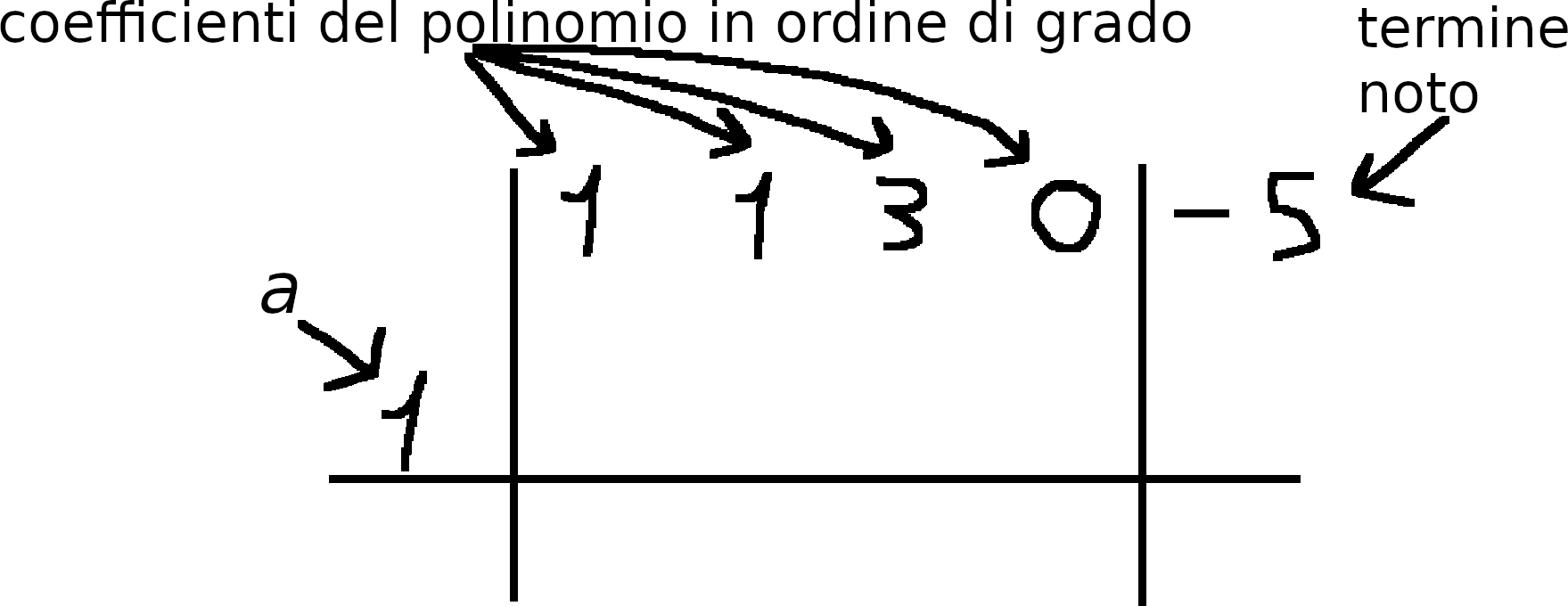
2. Si scrive il primo coefficiente sotto la linea orizzontale, si fa il prodotto fra tale coefficiente e il numero $a$ e si scrive sopra la linea orizzontale sotto il coefficiente di grado precedente:
   
   
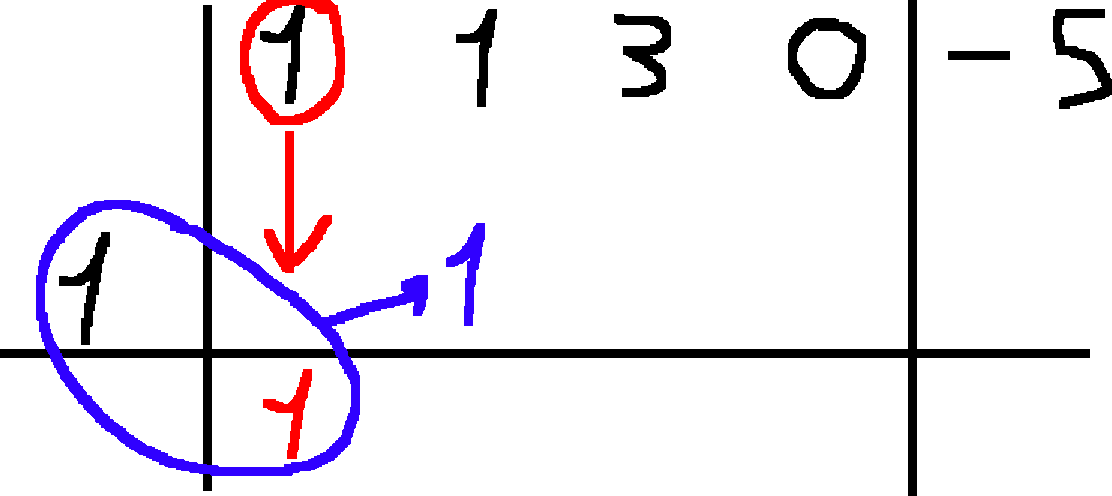
3. Si fa la somma fra il termine appena scritto e quello sopra di lui e si scrive tale risultato nella colonna accanto, sopra la linea orizzontale:
   
   
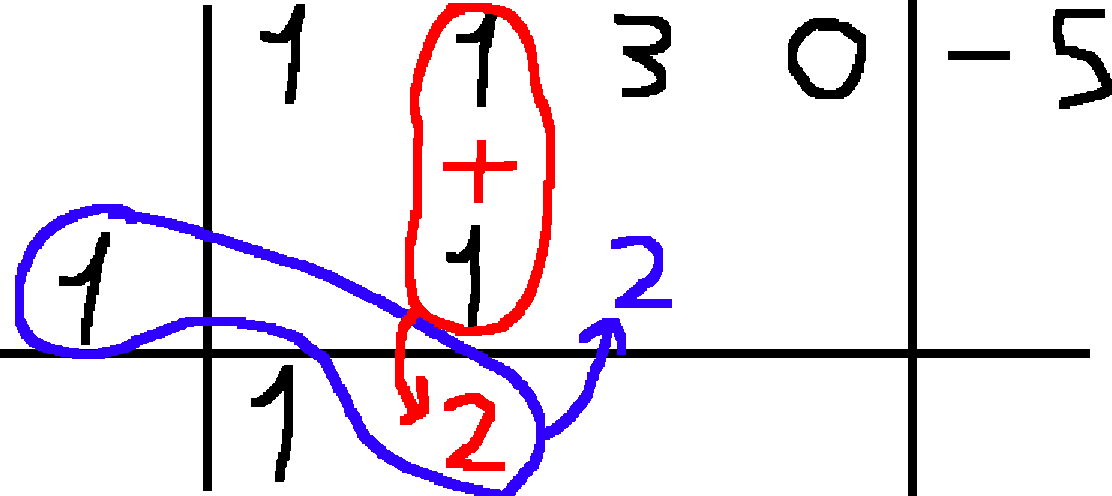
4. Si ripete il procedimento fino al termine noto.
   
   
   
   
   

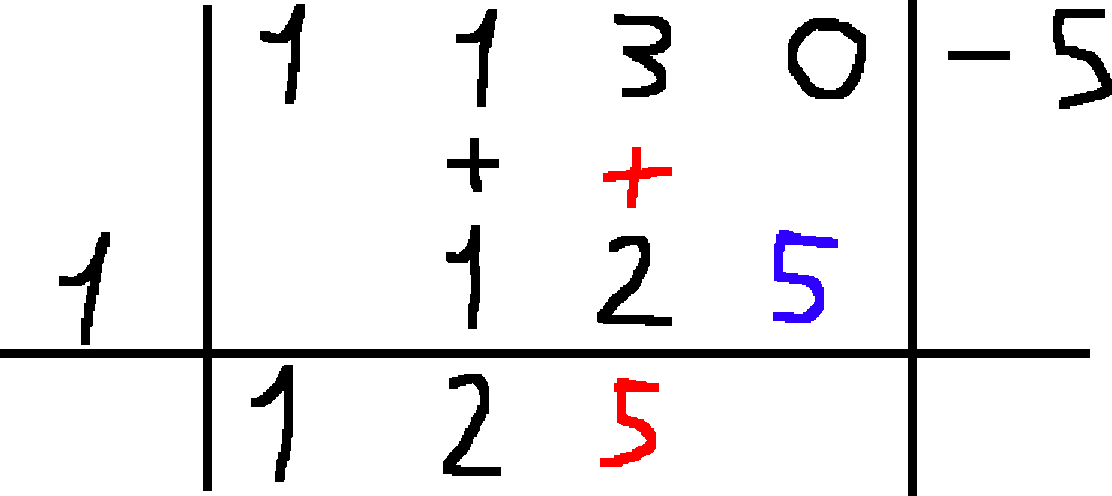
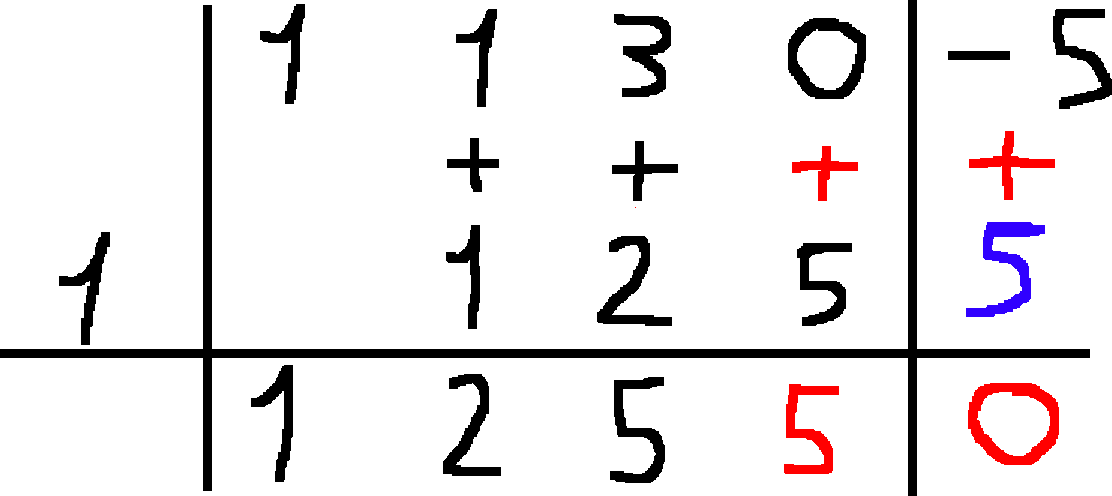
I numeri sotto la linea orizzontale sono i coefficienti del polinomio quoziente $Q(x)$, il cui grado sarà uno in meno rispetto ad $A(x)$.
Il resto $R(X)$ della divisione è costituito dal numero che sta in basso a destra della tabella. Nel nostro caso è venuto 0, per cui il polinomio $B(x)$ divide perfettamente $A(x)$.

Quindi dato che per definizione di divisione con resto fra polinomi si ha $A(x) = B(x)\cdot Q(x) + R(x)$, otteniamo: