Innanzitutto creiamo un sistema di assi cartesiani del filo che abbia come origine il centro del filo stesso
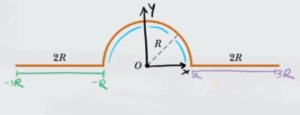
La carica totale del filo è data dal prodotto tra densità lineare e lunghezza totale $x$ del filo
$Q=λx$
Immaginiamo di dividere il filo in parti infinitamente piccole con carica $dQ$ data da
$dQ=λdx$
Per trovare il potenziale nel centro del filo dobbiamo calcolare il potenziale totale nel filo
$V=k\int_{-3R}^{3R}{\frac{dQ}{r}}$
Dividiamo l'integrale in 3 parti, una tra $-3R$ e $-R$, una lungo la semicirconferenza e una tra $R$ e $3R$
$V=k\int_{-3R}^{-R}{\frac{λ}{-x}dx}+\int_{Semicirc}^{ }{\frac{λ}{R}ds}+k\int_{R}^{3R}{\frac{λ}{x}dx}$
Dove $ds$ è il differenziale della circonferenza e il $-x$ nel primo integrale è presente perchè il primo tratto si trova a sinistra del nostro sistema di assi cartesiano, per cui è negativo.
L'integrale lungo il semicerchio è semplicemente l'integrale della semicirconferenza stessa
$k\int_{Semicirc}^{ }{\frac{λ}{R}ds}=k\frac{λ}{R}\int{ds}=k\frac{λ}{R}\cdot πR=kλπ$
Risolvendo anche gli altri integrali otteniamo
$V=kλln(-x)_{-3R}^{3R}+kλπ+kλln(x)_{R}^{3R}$
$V=kλln(3)+kλπ+kλln(3)=kλ(2ln(3)+π)$
