La densità di carica $σ$ è data dal rapporto tra carica totale e area del disco
$σ=\frac{Q}{A}$
Da questa equazione ricaviamo la carica del disco
$Q=σA$
Ora consideriamo una variazione infinitesimale di carica, cioè facciamo finta di dividere il disco in tanti cerchi concentrici infinitamente piccoli di area $dA$ e ad ognuno di questi cerchi associamo una carica $dQ$ data da
$dQ=σdA$
Sapendo che l'area del cerchio è $A=πr^2$, basta fare la derivata per trovare $dA=2πrdr$
$dQ=2πσrdr$
Sostituiamo il tutto nella formula del potenziale elettrico integrale
$V=k\int_{0}^{a}{\frac{dQ}{R}}$
La somma di tutti i cerchi concentrici parte dal centro del disco fino alle estremità, quindi dobbiamo integrare da 0 fino ad $a$ (cioè il raggio del disco).
$R$ rappresenta la distanza tra i vari cerchi e il punto P che stiamo considerando, come possiamo vedere dall'immagine è:
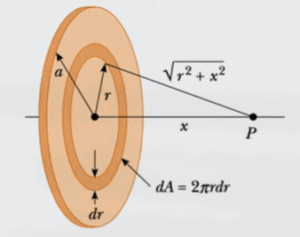
$R=\sqrt{r^2+x^2}$
Sostituendo il tutto all'interno dell'integrale otteniamo
$V=k\int_{0}^{a}{\frac{2πσrdr}{\sqrt{r^2+x^2}}}=2πkσ \int_{0}^{a}{\frac{rdr}{\sqrt{r^2+x^2}}}$
Risolvendo questo integrale otteniamo
$V=2πkσ(\sqrt{a^2+x^2}-x)$
Per trovare il campo elettrico basta fare la derivata del potenziale rispetto a $x$
$E=-\frac{dV}{dx}=2πkσ(1-\frac{x}{\sqrt{x^2+a^2}})$
