PRIMA DOMANDA
A $t=0$ la funzione d'onda si riduce a:
$y=0,3sin(2x+\frac{π}{4})$
Da questa funzione d'onda dobbiamo ricavare più informazioni possibili sull'onda armonica. Intanto la funzione seno è moltiplicata per $0,3$, questo numero rappresenta l'ampiezza dell'onda, cioè l'altezza.
$A=0,3m$
Quindi l'onda va da un massimo di altezza 0,3 metri fino a un minimo di -0,3 metri
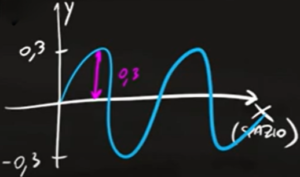
All'interno della funzione seno troviamo $2x$, il coefficiente che moltiplica $x$ è il numero d'onda $k$
$k=2$
Il numero d'onda rappresenta il numero di oscillazioni per unità di lunghezza ed è:
$k=\frac{2π}{λ}$
Sapendo che $k=2$ possiamo ricavare la lunghezza d'onda
$2=\frac{2π}{λ}$
$λ=\frac{2π}{2}=π$
La lunghezza d'onda è $π$ metri e rappresenta la lunghezza tra un picco e l'altro dell'onda
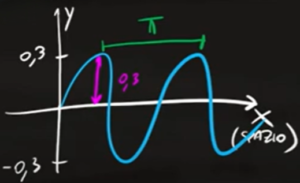
Infine all'interno della funzione seno:
$y=0,3sin(2x+\frac{π}{4})$
Il termine $2x$ è sommato a $π/4$. Questo termine noto all'interno della funzione seno rappresenta la fase inziale dell'onda, in pratica l'onda armonica non inizia dall'origine degli assi ma a sinistra dell'origine di $π/4$
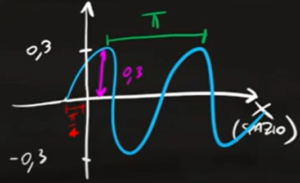
Questo è il grafico finale dell'onda.
SECONDA DOMANDA
Nel caso in cui il tempo è $t=0,2s$ la funzione d'onda diventa:
$y=0,3sin(2x-1+\frac{π}{4})$
Il grafico di questa onda è analogo al grafico dell'onda precedente con l'unica differenza che ora il termine noto è $-1+π/4$ che rappresenta sempre la fase iniziale
$φ=-1+\frac{π}{4}$
In questo grafico l'onda sarà spostata di $-1+π/4$ a sinistra rispetto all'origine degli assi
