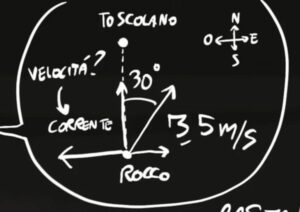
La velocità di rocco nel suo sistema di riferimento crea un angolo di 30° con l'asse Y, quindi possiamo scomporre la sua velocità
$v_x=vcos(30°)=3,03 m/s$
$v_y=vsin(30°)=1,75 m/s$
I sistemi di riferimento in questione sono due: il sistema di Rocco e quello di Zaccaria.
In questo problema la velocità della corrente rappresenta la velocità relativa tra i due sistemi di riferimento $v_{1;2}$ perché rappresenta l'unica grandezza che genera differenza tra la velocità di Rocco per Rocca e per Zaccaria.
La velocità di rocco per Rocco è la sua velocità vista da un sistema di riferimento interno, ed è $v_{A;1}. La velocità di Rocco per Zaccaria, invece, è la sua velocità da un punto di vista esterno, ed é $v_{A;2}.
Dalle trasformazioni di Galileo abbiamo che
$v_{A;2}=v_{A;1}+v_{1;2}$
Siccome la velocità di Rocco è divisa in componenti, possiamo scomporre anche la trasformazione di Galileo in due equazioni per i due assi (per semplicità sostituiamo la velocità di rocco per rocco con $v_r$, la velocità di Rocco per Zaccaria con $v_z$ e la velocità della corrente con $v_c$)
$v_{z_x }=v_{r_x}+v_{c_x}$
$v_{z_y}=v_{r_y}+v_{c_y}$
La corrente è orizzontale sull'asse X, quindi la componente Y è uguale a 0
$v_{z_x}=v_{r_x}+v_{c}$
$v_{z_y}=v_{r_y}$
In particolare a noi interessa solamente l'equazione della componente X, che contiene al suo interno la velocità della corrente
$v_{z_x}=v_{r_x}+v_c$
La velocità di Rocco per Zaccaria è lineare sull'asse Y, quindi la sua componente X è uguale a 0

Quindi l'equazione sull'asse X diventa
$0=v_{r_x}+v_{c}$
La velocità di rocco sull'asse X l'abbiamo ricavata all'inizio della pagina e risulta essere $v_{r_x}=1,75 m/s$.
$0=1,75 m/s +v_{c}$
$v_c=-1,75 m/s$
Il segno meno indica che il verso della corrente è opposta alla velocità orizzontale di Rocco.
