PAGINA DI TEORIA: Fenditure di Young
Le formule per la doppia fenditura di Young sono due:
$dsin(θ)=n\frac{λ}{2}$
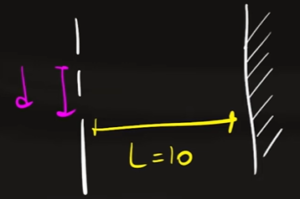
Dove $d$ è la distanza tra le due fenditure sul muro, $n$il numero della banda (chiara o scura), $λ$ è la lunghezza d'onda della luce e $θ$ è l'angolo che si crea tra il piano centrale e la banda che si sta considerando. La seconda equazione è la seguente:
$y=Ltan(θ)$
Dove $θ$ è lo stesso angolo di prima, $L$ è la distanza tra il muro e lo schermo posto dietro su cui vengono proiettate le bande luminose e $y$ la distanza tra la banda centrale e la banda che si sta considerando.
SINGOLA FENDITURA
Per la singola fenditura la prima equazione diventa:
$dsin(θ)=nλ$
Dove $θ$, $λ$ ed $n$ sono gli stessi di prima, con l'unica differenza che $d$ ora rappresenta la lunghezza della fenditura.
L'altra equazione rimane identica a quella della doppia fenditura
$y=Ltan(θ)$
- Esercizio 1
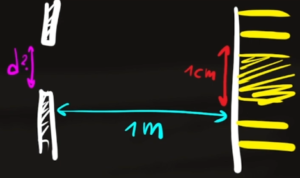
Una fenditura singola è posta a 1 metro di distanza da uno schermo su cui le prime due bande scure sono proiettate a 1 centimetro di distanza l'una dall'altra. Sapendo che la lunghezza d'onda della luce è $λ=680$ $nm$ calcola la lunghezza della fenditura
- Esercizio 2
Un raggio luminoso di lunghezza d'onda $λ=560$ $nm$ attraversa una singola fenditura di lunghezza $d=1$ $μm$. Quanto vale l'angolo di inclinazione $θ$ rispetto alla banda centrale per la prima e la seconda banda scura?
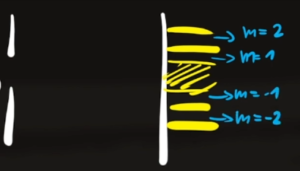
- Esercizio 3
Un raggio luminoso di lunghezza d'onda $λ=200$ $nm$ attraversa una doppia fenditura in cui la distanza tra le due fenditure è $d=2$ $cm$. Sapendo che la distanza tra la doppia fenditura e lo schermo posto dietro è $L=2m$ trova la posizione della 1° banda chiara e della 3° banda scura
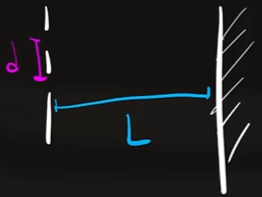
- Esercizio 4
Un raggio luminoso attraversa una doppia fenditura la cui distanza tra le due fenditure è $d=2$ $cm$ e la distanza tra la fenditura e lo schermo posto dietro è $L=10$ $m$. Sapendo che la distanza tra le prime due bande chiare è $8$ $μm$ e che la distanza tra le seconde bande scure è $12$ $μm$ calcola la lunghezza d'onda del raggio luminoso.
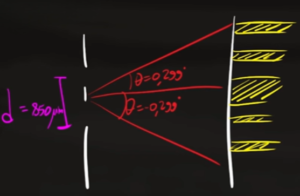
- Esercizio 5
Un raggio luminoso di lunghezza d'onda $λ=633$ $nm$ attraversa una doppia fenditura la cui distanza tra le due fenditure è $d=850$ $μm$. Vengono individuate due bande chiare simmetriche che si trovano ad un angolo $θ_1=0,299°$ e $θ_2=-0,299°$ di inclinazione rispetto alla banda chiara centrale. Calcola il numero delle due bande