La forza magnetica di un filo su una spira è data da
$F=i_slBsin(θ)$
Dove il campo $B$ prodotto dal filo cambia in base al lato della spira che stiamo considerando dato che hanno tutti distanze diverse dal filo.
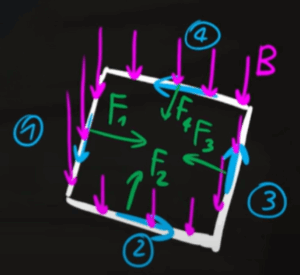
In questa immagine sono rappresentate le varie forze magnetiche prodotte all'interno della spira. Il campo magnetico è perpendicolare alla spira, quindi possiamo porre il seno dell'angolo uguale a 1
$F=i_slB$
Le forze 2 e 4 sono uguali tra loro perché si trovano alla stessa distanza dal filo e hanno versi opposti, quindi la loro somma è uguale a 0. Dato che le forze 2 e 4 si annullano la forza totale è data solo dalla somma della forza 1 e 3
$F=F_1-F_3=i_slB_1-i_slB_3$
$F=i_sl(B_1-B_3)$
Il segno meno va inserito perché le due forze hanno versi opposti. Il campo magnetico del filo sulla spira è dato dalla formula
$B=\frac{μ_0i_f}{2πr}$
La distanza di 1 metro che ci viene data dal problema è la distanza tra il filo e il centro della spira, quindi la distanza tra il lato 1 il filo è la lunghezza del filo dal centro meno metà del lato
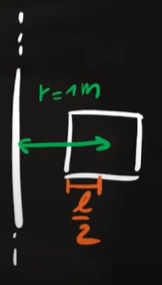
$r_1=1-\frac{l}{2}$
Mentre il lato 3, più distante, dista 1 metro più metà del lato
$r_3=1+\frac{l}{2}$
Quindi la somma dei due campi magnetici è:
$B_1-B_3=\frac{μ_0i_f}{2π(1-l/2)}-\frac{μ_0i_f}{2π(1+l/2)}$
$B_1-B_3=\frac{μ_0i_f}{2π}\cdot \frac{4l}{4-l^2}$
Quindi la forza totale agente sulla spira è:
$F=i_sl(B_1-B_3)=i_sl\cdot \frac{2lμ_0i_f}{π(4-l^2)}$
Sostituendo i valori otteniamo:
$F=10^{-6}N$
