Dall'esercizio 2 abbiamo calcolato il campo magnetico del solenoide. Al centro sono presenti due campi magnetici, il campo prodotto dal solenoide stesso che lo attraversa in orizzontale e il campo magnetico esterno che lo attraversa in verticale
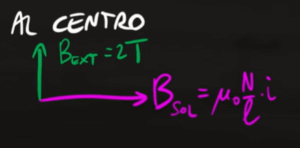
Quindi il campo magnetico totale è dato dalla somma vettoriale di questi due campi magnetici. I due vettori di campo formano un angolo di 90° tra di loro, quindi la loro somma vettoriale è data dal teorema di Pitagora
$B_{TOT}=\sqrt{B_{in}^2+B_{ext}^2}$
Sapendo che $B_{in}=1,5\cdot 10^{-4}$ $T$ e $B_{ext}=2T$ otteniamo
$B_{TOT}=2T$
