Per calcolare il campo magnetico di tutto il circuito possiamo utilizzare la legge di Laplace considerando una porzione infinitamente piccola di circuito
$dB=\frac{μ_0i}{2πr}\cdot \frac{dl×r}{r^3}$
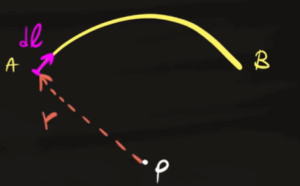
Dove $r$ rappresenta la distanza tra $dl$ e il centro P.
Per trovare il campo magnetico basta applicare l'integrale lungo il circuito alla formula mostrata prima, ma prima di farlo possiamo eliminare i campi $B_{DA}$ e $B_{BC}$ perché hanno la stessa distanza dal centro e hanno correnti opposte.
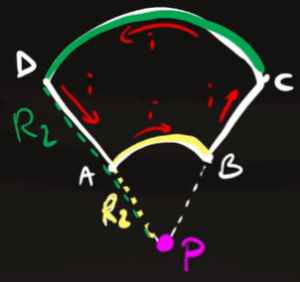
Quindi il campo magnetico totale è dato solamente dalla somma dei campi dei due archi AB e CD
$B=\int_{A}^{B}dB_{AB}+\int_{C}^{D}dB_{CD}$
Se si considera una porzione infinitamente piccola dell'arco di circonferenza questa si può approssimare ad una linea retta, quindi l'angolo tra la distanza con il centro e questo segmento infinitamente piccolo è 90°
$dl×r=dl\cdot rsin(90°)=dl\cdot r$
Quindi la formula del campo magnetico diventa
$dB=\frac{μ_0i}{2πr}\cdot \frac{dl}{r^2}$
Sostituendo questa formula nell'integrale otteniamo
$B=\frac{μ_0i}{2πr}(\frac{1}{r_{1}^2}\int_{A}^{B}dl+\frac{1}{r_{2}^2}\int_{C}^{D}dl)$
I due integrali che sono rimasti da risolvere rappresentano semplicemente le lunghezze degli archi AB e CD, che si possono trovare considerando l'angolo che formano con il centro
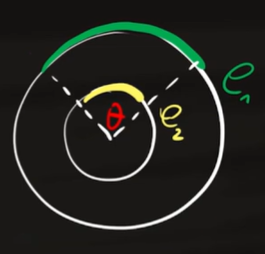
Dall'immagine vediamo le proiezioni dei due archi che formano due circonferenze di raggio $r_1$ e $r_2$. Da qui possiamo scrivere una proporzione tra l'arco che ci interessa e tutta la circonferenza. In particolare possiamo scrivere una proporzione tra l'arco e il suo angolo rispetto alla circonferenza
$AB:θ=2πr_1:2π$
$AB=θr_1$
La stessa proporzione vale anche per CD
$CD=θr_2$
Sostituendo queste due lunghezze al posto degli integrali otteniamo l'espressione del campo magnetico in funzione dell'angolo θ
$B=\frac{μ_0i}{2πr}(\frac{θr_1}{r_{1}^2}+\frac{θr_2}{r_{2}^2})$
Semplificando il numeratore con il denominatore si ottiene
$B=\frac{μ_0i}{2πr}(\frac{θ}{r_1}+\frac{θ}{r_2})$
