Per trovare la forza totale agente sul protone dobbiamo sommare vettorialmente le due forze agenti; la forza elettrica e la forza magnetica
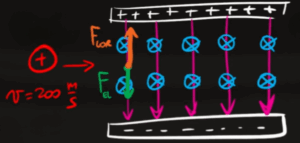
Come si può vedere dall'immagine la forza elettrica punta verso il basso (perché il protone è attratto dalla piastra negativa che si trova in basso) mentre la forza magnetica è rivolta verso l'alto.
La direzione della forza magnetica la si può trovare con la regola della mano destra sapendo che deve essere perpendicolare sia al campo elettrico che al moto del protone, come risultato si ha che la forza magnetica è rivolta verso l'alto.
Dato che le due forze sono opposte, la forza totale sarà la differenza delle due
$F_{TOT}=F_{lor}-F_{el}$
La forza elettrica è semplicemente il prodotto tra il campo elettrico e la carica del protone ($q=1,6\cdot 10^{-19}C$)
$F_{el}=Eq=6,4\cdot 10^{-19}N$
La forza magnetica invece la possiamo ricavare con la formula di Lorentz in cui il seno dell'angolo tra il campo magnetico e il moto del protone è 1 perché sono perpendicolari
$F_{lor}=qvB=1,28\cdot 10^{-16}N$
Facendo la differenze tra le due otteniamo
$F_{TOT}=F_{el}-F_{lor}=-1,28\cdot 10^{-16}N$
Il segno meno indica che tra le due forze prevale la forza magnetica e il moto del protone sarà influenzata da essa.
