Per il teorema di Gauss sappiamo che il flusso di campo elettrico che passa per una superfice chiusa è:
$Φ=\frac{Q_{TOT}}{ε_0}$
Dove $Q_{TOT}$ è la carica totale presente nella superfice.
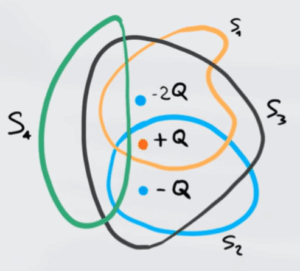
Nella superfice 1 (gialla) sono presenti due cariche, $-2Q$ e $Q$, la carica totale quindi è $Q_{TOT}=-Q$. Di conseguenza il flusso di campo è
$Φ_1=-\frac{Q}{ε_0}$
Nella superfice 2 (blu) invece sono presenti le due cariche $-Q$ e $Q$ e la carica totale è $Q_{TOT}=Q-Q=0$
$Φ_2=\frac{0}{ε_0}=0$
Nella superfice 3 (grigia) sono presenti tutte e tre le cariche, quindi la carica totale è $Q_{TOT}=-2Q+Q-Q=-2Q$
$Φ_3=-\frac{2Q}{ε_0}$
Nella superfice 4 (verde) non è presente nessuna carica, di conseguenza il flusso è nullo
$Φ_4=0$
