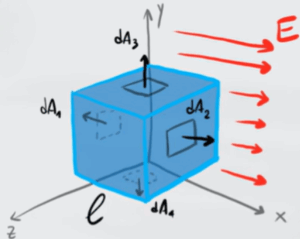
Dall'immagine del cubo possiamo vedere che le facce 3 e 4 sono perpendicolari al campo elettrico, di conseguenza il flusso di campo elettrico è nullo in queste due superfici.
$Φ=E\cdot S\cdot cos(90°)=0$
La stessa cosa anche per le due facce del cubo non numerate. Quindi le uniche due facce del cubo che sono soggette ad un flusso di campo sono le facce 1 e 2.
Sulla faccia 1 la direzione del campo elettrico è opposta alla superfice e forma un angolo di 180° con essa, quindi il flusso è:
$Φ_1=E\cdot S\cdot cos(180°)$
Sapendo che la superfice del cubo è semplicemente $l^2$ e che il coseno di 180° è -1 otteniamo
$Φ=-El^2$
Per quanto riguarda la faccia 2, il campo elettrico punta nella stessa direzione della superfice e forma un angolo di 0° con essa.
$Φ_2=El^2\cdot cos(0°)=El^2$
Quindi il flusso di campo elettrico totale sulla superfice è:
$Φ=Φ_1+Φ_2=-El^2+El^2=0$
Il flusso totale risulta 0, ciò implica che il campo elettrico entra all'interno del cubo con la stessa intensità con cui esce.
