PAGINA DI TEORIA: Flusso elettrico
Il flusso di campo elettrico su una superfice si calcola come il prodotto scalare tra il campo elettrico e la superfice stessa
$Φ=E\cdot A\cdot cos(θ)$
Dove $θ$ è l'angolo tra la superfice e la direzione del campo.
La versione integrale del flusso è:
$Φ=\int{E\cdot dA}$
Per il teorema di Gauss il flusso lungo una superfice chiusa è:
$Φ=\frac{Q}{ε_0}$
- Esercizio 1
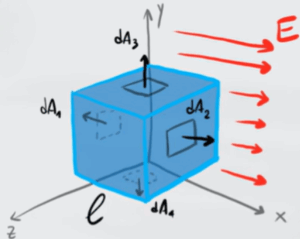
Un cubo di lato $l$ è soggetto ad un campo elettrico di direzione e verso mostrati in figura. Calcola il flusso di campo che attraversa il cubo
- Esercizio 2
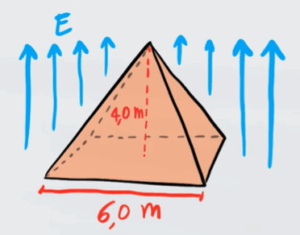
Una piramide di altezza $h=4m$ e di base quadrata di lato $l=6m$ è soggetta ad un campo elettrico perpendicolare alla base e rivolto verso l'alto di intensità $E=52$ $N/C$. Quanto vale il flusso di campo elettrico lungo le 4 facce laterali?
- Esercizio 3
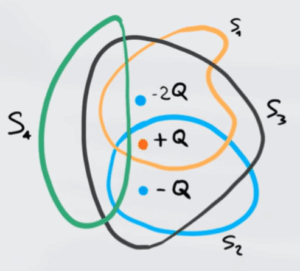
Le cariche $-Q$ , $+Q$ e $-2Q$ sono distribuite in 4 superfici come mostrato in figura. Calcola il flusso di campo elettrico lungo ogni superfice
- Esercizio 4
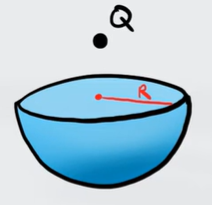
Una carica $Q$ è posta sopra il centro di una semisfera di raggio $R$. Quanto vale il flusso lungo la superfice piana e curva della sfera?
- Esercizio 5
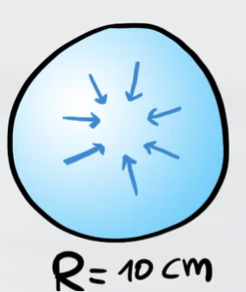
Una sfera di raggio $R=10$ $cm$ ha una densità di carica uniforme e al suo interno è presente un campo elettrico che ha come direzione il centro della sfera. Il campo elettrico ha intensità $E=86$ $kN/C$ a $5$ $cm$ dal centro. Quanto vale il campo elettrico ad una distanza $d=15$ $cm$ dal centro?
- Esercizio 6 (teorema di Gauss applicato al potenziale elettrico)
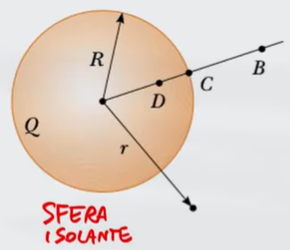
Una sfera isolante di raggio $R$ ha una carica totale positiva $Q$.
a) Trova il potenziale elettrico in un punto fuori dalla sfera di distanza $r$ dal centro
b) Trova il potenziale elettrico all'interno della sfera