FORZA AGENTE SULLA CARICA 2
La forza totale elettrica agente sulla carica 2 si può calcolare con la formula
$F=q_2\cdot E_{tot}$
Per trovare il campo elettrico totale percepito dalla carica $q_2$ dobbiamo calcolare i campi elettrici delle cariche $q_1$ e $q_3$
$E_1=\frac{Kq_1}{a^2}=2,25\cdot 10^6$ $N/C$
$E_3=\frac{Kq_3}{a^2}=2,25\cdot 10^6$ $N/C$
NOTA: ricordati di convertire le unità di misura delle cariche elettriche in Coulomb ($q_1=q_3=10^{-5}$ $C$)
Il campo elettrico della carica 1 è rivolto verso il basso (perché è diretto verso la carica negativa $q_2$) mentre la carica 3 è rivolta verso sinistra (sempre perché è diretta verso la carica $q_2$ che ha segno opposto)
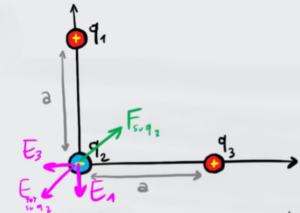
I due vettori di campo elettrico sono perpendicolari tra loro, quindi possiamo trovare il campo elettrico totale utilizzando il teorema di Pitagora
$E_{tot}=\sqrt{E_{1}^2+E_{3}^2}$
Da qui possiamo ricavare la forza totale agente sulla carica $q_2$ usando la formula mostrata all'inizio
$F=q_2\cdot E_{tot}=3,2$ $N$
FORZA AGENTE SULLA CARICA 3
Per la carica 3 dobbiamo fare un procedimento simile alla carica 2, per prima cosa troviamo i campi elettrici generati dalle altre due cariche
$E_2=\frac{K|q_1|}{a^2}=2,25\cdot 10^6$ $N/C$
Il campo elettrico della carica 1 è diversa poiché la distanza ora non è più $a$ ma è la diagonale del triangolo rettangolo che si è formato in figura che ha come cateti $a$
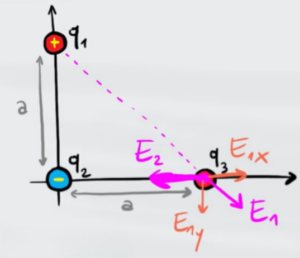
Usando il teorema di Pitagora otteniamo che la distanza tra la carica 1 e la carica 3 è:
$d=a\sqrt{2}$
Quindi il campo elettrico della carica 1 percepito dalla carica 3 è:
$E_1=\frac{Kq_1}{2a^2}=1,12\cdot 10^{6}$ $N/C$
Come si vede dalla figura, il campo elettrico della carica 2 è lungo l'asse X mentre il campo elettrico della carica 1 è in diagonale per cui ha una componente X e una componente Y. Siccome il triangolo rettangolo in figura ha i cateti congruenti ha sicuramente l'angolo alla base di 45°
$E_{1x}=E_1cos(45°)=7,92\cdot 10^5$ $N/C$
$E_{1y}=E_1sin(45°)=7,92\cdot 10^5$ $N/C$
Il campo elettrico lungo X della carica 1 genera una forza repulsiva perché la carica 1 ha lo stesso segno della carica 3, quindi è diretto verso destra. Il campo elettrico della carica 2, invece, è sempre lungo l'asse X ma a differenza della carica 1 genera una forza attrattiva dato che la carica 2 ha segno opposto della carica 3 (quindi il campo elettrico è diretto verso sinistra).
Siccome i due campi elettrici lungo l'asse X sono opposti, possiamo trovare il campo elettrico totale lungo l'asse X facendo la differenza dei due campi
$E_{TOT_x}=E_{1x}-E_2=-1,46\cdot 10^{6}$ $N/C$
Il segno meno indica che è rivolto verso sinistra. Il campo elettrico totale lungo l'asse Y, invece, è dato solamente dal campo elettrico lungo l'asse Y della carica 1
$E_{TOT_y}=E_{1y}=7,92\cdot 10^5$ $N/C$
Ora possiamo calcolare il campo elettrico totale percepito dalla carica 3 utilizzando il teorema di Pitagora
$E_{TOT}=\sqrt{E_{TOT_x}^2+E_{TOT_y}^2}$
$E_{TOT}=1,66\cdot 10^{6}$ $N/C$
Ora che abbiamo calcolato il campo elettrico totale possiamo ricavare la forza agente sulla carica 3 moltiplicando il campo elettrico per la carica $q_3$
$F=E_{TOT}\cdot q_3=16,6N$
