Per prima cosa scegliamo il nostro sistema di riferimento in cui il corpo 1 si trova all'origine degli assi
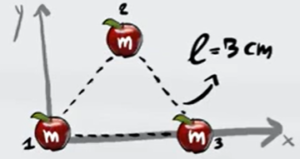
Per prima cosa troviamo le coordinate X del centro di massa usando la formula generale
$X_{CM}=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}$
Il corpo 1 si trova all'orine degli assi, quindi la sua posizione sull'asse X è $x_1=0$, il corpo 2 invece si trova a metà tra il corpo 1 e il corpo 3, quindi la sua distanza dall'origine è metà lato del triangolo
$x_2=\frac{l}{2}=1,5cm$
La distanza tra il corpo 3 e l'origine è tutto il lato del triangolo, quindi $x_3=3cm$. Sostituendo i dati nel centro di masso otteniamo:
$X_{CM}=\frac{1,5m_2+3m_3}{m_1+m_2+m_3}$
I corpi hanno tutti e 3 massa uguale, quindi possiamo raccogliere le masse
$X_{CM}=\frac{4,5m}{3m}=\frac{4,5}{3}=1,5cm$
CENTRO DI MASSA SULL'ASSE Y
Sull'asse Y il centro di massa ha la stessa formula con le coordinate y
$Y_{CM}=\frac{m_1y_1+m_2y_2+m_3y_3}{m_1+m_2+m_3}$
Il corpo 1 si trova all'origine, quindi la sua posizione sull'asse Y è $y_1=0$. Il corpo 3 si trova interamente sull'asse X, quindi la sua posizione sull'asse Y è $y_3=0$.
Il corpo 2, invece, ha come posizione sull'asse Y l'altezza del triangolo equilatero, quest'ultima la possiamo ricavare utilizzando il teorema di Pitagora.
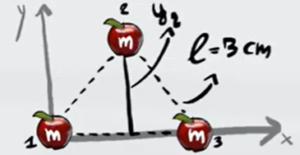
Dalla figura possiamo vedere che tagliando a metà la base si forma un triangolo rettangolo in cui l'ipotenusa è il lato del triangolo mentre l'altro cateto è metà della base. Dalla formula del teorema di Pitagora possiamo ricavare l'altezza
$y_2=\sqrt{l^2-(\frac{l}{2})^2}=\sqrt{l^2-\frac{l^2}{4}}$
Semplificando i termini otteniamo:
$y_2=\sqrt{l^2\frac{3}{4}}=l\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}$
Sostituiamo i valori ottenuti nella formula del centro di massa Y
$Y_{CM}=\frac{\frac{3\sqrt{3}}{2}m_2}{m_1+m_2+m_3}$
Siccome le masse sono uguali le possiamo sommare tra loro
$Y_{CM}=\frac{\frac{3\sqrt{3}}{2}m}{3m}=\frac{\sqrt{3}}{2}$ $cm$
Mettendo insieme le coordinate X e Y ricavate otteniamo che il centro di massa è un vettore con le seguenti coordinate:
$r_{CM}=(1,5,\frac{\sqrt{3}}{2})$
