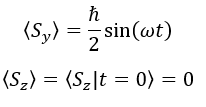Ogni particella ha uno spin positivo e uno spin negativo e può avere mezza probabilità di trovarsi in uno e mezza probabilità di trovarsi nell’altro e, a seconda dello spin in cui si trova la particella, può avere funzioni d’onda differenti.
L’hamiltoniana di una particella è direttamente proporzionale allo spin della stessa particella:
![]()
Quindi possiamo riscrivere l’equazione d’onda di Schroedinger (stiamo prendendo in considerazione una particella con spin semi intero) in questo modo:
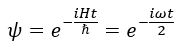
La funzione d’onda dipende dal verso di rotazione (cioè dal segno dello spin)
![]()
La probabilità di avere la particella in uno dei due stati è ½ e ½ quindi scriviamo la probabilità usando le due funzioni d’onda che abbiamo appena definito
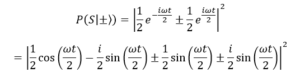
Quindi abbiamo ottenuto due equazioni della probabilità per i due stati di spin
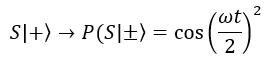
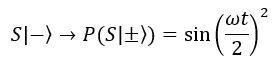
Possiamo ricavare il valore medio dello spin lungo l’asse x facendo la somma tra la probabilità di S+ e la probabilità di S-, tutto moltiplicato per lo spin a t = 0 (a t = 0 lo spin è h/2):
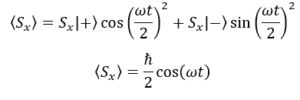
In questo modo ricaviamo anche i valori medi dello spin sull’asse y e z: