Gottfried Wilhelm Leibniz nacque il 1º luglio 1646 a Lipsia, in Sassonia, nel cuore della Germania protestante. Sin dalla prima infanzia dimostrò un'intelligenza fuori dal comune, tanto che a soli 12 anni padroneggiava il latino e leggeva i classici greci in lingua originale. Era figlio di un professore di filosofia morale, che morì quando lui aveva appena sei anni. Questo evento spinse il giovane Leibniz a cercare rifugio nei libri e nello studio, crescendo come un autodidatta brillante e instancabile.
La sua formazione fu ampia e interdisciplinare: studiò filosofia, diritto, matematica, fisica, teologia, storia e lingue, incarnando pienamente l’ideale del “polimatematico” barocco, ovvero dell’uomo che aspira a conoscere tutto lo scibile umano. Si laureò in legge a soli 20 anni all’Università di Altdorf, dopo essere stato rifiutato dall’Università di Lipsia per motivi politici e religiosi.

Università di Altdorf
Dopo la laurea, Leibniz venne coinvolto in incarichi diplomatici e giuridici al servizio di vari principi tedeschi. Queste esperienze gli permisero di viaggiare in tutta Europa e di entrare in contatto con alcuni dei più grandi scienziati e intellettuali del tempo: tra cui Christiaan Huygens, Robert Boyle, Isaac Newton, Baruch Spinoza, e John Locke. Si inserì così al centro della “Repubblica delle Lettere”, la rete europea degli intellettuali del XVII secolo.
Uno dei suoi periodi più importanti fu il soggiorno a Parigi (1672–1676), dove approfondì la matematica e le scienze naturali, e dove entrò in competizione (non senza polemiche) con gli ambienti scientifici inglesi, soprattutto con Newton. Fu proprio in questi anni che sviluppò, in modo indipendente da Newton, il calcolo infinitesimale.
Nel 1676 si trasferì a Hannover, dove avrebbe trascorso il resto della sua vita come bibliotecario e consigliere di corte per la famiglia dei duchi di Brunswick-Lüneburg. Nonostante gli impegni politici e amministrativi, Leibniz non abbandonò mai la ricerca. Continuò a scrivere, a progettare invenzioni meccaniche, a studiare storia, logica, geologia, medicina e persino a tentare di unificare il sapere umano in un grande sistema enciclopedico.
Durante la sua vita, cercò anche di mediare tra le diverse confessioni religiose cristiane, convinto che l’unità del sapere dovesse riflettersi anche nell’unità spirituale dell’umanità. Propose progetti visionari come la creazione di un’accademia delle scienze universale e una lingua simbolica perfetta, anticipando molte delle idee alla base della logica matematica e dell’informatica moderna.
Morì ad Hannover il 14 novembre 1716, quasi ignorato dalla corte che aveva servito fedelmente per quarant’anni. Nonostante il suo ruolo ufficiale e il suo prestigio intellettuale, al suo funerale parteciparono soltanto il suo segretario e pochi amici. L’Accademia delle Scienze di Berlino, da lui stesso fondata, non inviò neppure una delegazione. Eppure, la grandezza di Leibniz non fu cancellata dal silenzio dei suoi contemporanei. Nei secoli successivi, il suo pensiero è stato riscoperto, studiato e ammirato da matematici, filosofi, logici e informatici. Oggi è considerato uno dei più grandi geni del pensiero occidentale, capace di spaziare con profondità e originalità in ogni ambito del sapere umano.
L’architetto invisibile della matematica moderna
Quando, negli ultimi decenni del Seicento, Gottfried Wilhelm Leibniz iniziò a elaborare i primi concetti di quella che oggi chiamiamo analisi matematica, l’Europa era ancora dominata dalla geometria euclidea e dalla fisica cartesiana. La matematica era più uno strumento al servizio della filosofia naturale che un linguaggio autonomo e universale. Ed è proprio questo che Leibniz volle cambiare. La sua ambizione non era soltanto scoprire nuove formule, ma costruire un sistema simbolico che potesse rendere la conoscenza calcolabile.
Il suo nome è oggi indissolubilmente legato all’invenzione del calcolo infinitesimale, sviluppato in modo indipendente da quello di Newton. Ma l’approccio di Leibniz si rivelò radicalmente diverso: là dove Newton procedeva con intuizioni geometriche e fisiche, Leibniz adottava un metodo algebrico e simbolico, basato sull’uso sistematico di entità infinitamente piccole — i differenziali dx e dy.
Questi differenziali erano pensati come quantità infinitesime, la cui divisione rappresentava un rapporto di variazione istantanea: per una funzione y = f(x), il rapporto dy/dx indicava la pendenza della tangente alla curva in un punto. Sebbene la teoria dei limiti non fosse ancora formalizzata (ciò avverrà solo nell’Ottocento), Leibniz riuscì comunque a operare con queste entità in modo coerente, fondando un intero sistema di calcolo.
A rendere straordinario il suo contributo fu la notazione, che sopravvive intatta ancora oggi. L’introduzione del simbolo ∫ per l’integrale, ispirato alla “S” di summa, rifletteva la visione dell’integrale come somma continua di infiniti differenziali. L’integrale definito, che calcola l’area sotto una curva y = f(x) tra due estremi a e b, veniva dunque scritto come:
∫ab f(x) dx
L’eleganza e la potenza della notazione leibniziana divennero centrali nello sviluppo dell’analisi matematica del XVIII e XIX secolo. Ma Leibniz andò ben oltre l’aspetto operativo: egli intuì che la derivata e l’integrale sono operazioni inverse. Questa intuizione è il nucleo del cosiddetto teorema fondamentale del calcolo, un concetto che sarà rigorosamente formulato solo in seguito, ma che già nella visione di Leibniz permetteva di collegare dinamicamente l’analisi locale (variazione) con l’analisi globale (accumulazione).
Parallelamente, il filosofo-matematico si interessò alle serie infinite e ai metodi per rappresentare funzioni o costanti notevoli come somma di infiniti termini. Un esempio celebre è la serie di Leibniz per π:
π/4 = 1 - 1/3 + 1/5 - 1/7 + ⋯
Questa formula, sebbene converga molto lentamente, mostra come Leibniz stesse cercando una struttura algebrica per le grandezze geometriche, trasformando il calcolo delle aree o delle lunghezze in problemi di manipolazione simbolica. La matematica, per lui, non era un insieme di ricette: era una grammatica del mondo.
Tuttavia, una delle sue idee più visionarie fu il sistema numerico binario, che illustrò nel saggio del 1703 Explication de l'Arithmétique Binaire. Mentre il mondo scientifico utilizzava il sistema decimale, Leibniz mostrava che con solo due cifre — 0 e 1 — era possibile rappresentare qualsiasi numero intero. Oggi il principio è banale, ma all’epoca appariva quasi mistico. Leibniz arrivò perfino a interpretare simbolicamente l’1 come Dio e lo 0 come il nulla: tutta la creazione, sosteneva, può emergere da questa semplice opposizione.
In termini matematici, il binario si basa sulla rappresentazione posizionale: ad esempio, il numero decimale 13 si scrive in binario come 11012, ovvero:
1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 8 + 4 + 0 + 1 = 13
Questo sistema non era solo un gioco logico: era la base teorica per la costruzione di macchine calcolatrici automatiche, che Leibniz tentò di realizzare con la sua Stepped Reckoner. La macchina, progettata negli anni ’70 del Seicento, utilizzava una ruota dentata (poi chiamata “ruota di Leibniz”) per realizzare moltiplicazioni e divisioni meccaniche. Sebbene tecnicamente fragile, l’idea anticipava in modo diretto i principi dei calcolatori meccanici dell’Ottocento e dei computer elettronici del Novecento.
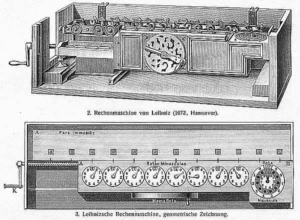
Macchina calcolatrice di Leibniz, nominata Stepped Reckoner - 1671
A coronare tutto ciò vi è il sogno forse più ambizioso di Leibniz: quello di una lingua universale del pensiero, in cui tutte le proposizioni potessero essere scritte come formule e risolte attraverso un calcolo meccanico. Egli chiamava questa idea characteristica universalis, un linguaggio logico-matematico che avrebbe permesso di decidere la verità di qualsiasi affermazione tramite puro calcolo. Il motto con cui riassumeva questa visione era semplice e potente: “Calculemus!” — “calcoliamo!”
Questa intuizione, apparentemente utopica, anticipava di oltre due secoli i fondamenti della logica simbolica, della teoria della computabilità e dell’intelligenza artificiale. In effetti, matematici come Boole, Frege, Russell e infine Turing riconobbero in Leibniz un predecessore assoluto del pensiero algoritmico.
Epigrafe dell’eternità
Se oggi scriviamo un integrale come ∫f(x) dx, se calcoliamo con computer binari, se crediamo che un problema possa essere risolto tramite algoritmo, è perché Leibniz ha saputo vedere, nei simboli, una seconda realtà — invisibile, ma altrettanto concreta. La sua matematica non fu un semplice strumento, ma un linguaggio filosofico, una forma di pensiero puro e universale. Il mondo contemporaneo, digitale, formale, algoritmico, deve a lui più di quanto sia comunemente noto. Leibniz non fu solo un matematico: fu l’architetto di un nuovo modo di pensare.







