L’Hotel di Hilbert è un famoso esperimento mentale ideato da David Hilbert per esplorare le proprietà controintuitive dell’infinito numerabile. In questo articolo analizziamo i casi classici del paradosso e introduciamo un’estensione meno nota ma fondamentale: l’arrivo di infinite persone con nomi costituiti da infinite lettere scelte a caso. Mostreremo che, a differenza dei casi precedenti, qui si entra nel dominio dell’infinito non numerabile, e che l’hotel — pur essendo infinitamente grande — non ha più spazio sufficiente. Innanzitutto, chi era Hilbert?

Chi era Hilbert?

David Hilbert (1862–1943) è stato uno dei più grandi matematici della storia, una figura centrale nella transizione verso la matematica moderna. Nato il 23 gennaio 1862 a Königsberg, in Prussia orientale (oggi Kaliningrad, Russia), mostrò fin da giovane una straordinaria predisposizione per il pensiero astratto. Studiò all’Università di Königsberg, dove si formò sotto la guida di matematici del calibro di Ferdinand von Lindemann e Adolf Hurwitz. Dopo aver completato il dottorato nel 1885 con una tesi sulla teoria degli invarianti, Hilbert intraprese una carriera accademica che lo portò, nel 1895, all’Università di Göttingen, allora uno dei più prestigiosi centri di ricerca matematici al mondo.

Hilbert non fu solo uno scienziato brillante, ma anche un eccezionale mentore. Tra i suoi allievi e collaboratori si annoverano figure che
avrebbero lasciato un’impronta indelebile nella matematica e nella fisica teorica, come Hermann Weyl, Ernst Zermelo, John von Neumann e il giovane Kurt Gödel. A Göttingen, Hilbert trasformò il dipartimento di matematica in un ambiente intellettualmente fertile, contribuendo a
renderlo la culla di molte rivoluzioni scientifiche del Novecento.

Uno dei suoi contributi più significativi fu lo sviluppo del metodo assiomatico, applicato inizialmente alla geometria. Nel 1899, con la pubblicazione di Grundlagen der Geometrie (I fondamenti della geometria), Hilbert rivoluzionò il modo in cui si concepiva la struttura logica della matematica.
A differenza degli Elementi di Euclide, Hilbert mise in evidenza la necessità di esplicitare tutti gli assiomi e costruire la teoria su basi
rigorosamente formali, evitando qualsiasi presupposto implicito.

Nel 1900, al Congresso Internazionale dei Matematici di Parigi, Hilbert presentò un elenco di 23 problemi irrisolti, destinati a orientare il lavoro matematico del secolo a venire. Questi “Problemi di Hilbert” affrontavano questioni fondamentali in ambiti diversi: dall’aritmetica alla geometria, dall’analisi alla fisica matematica. La visione di Hilbert culminò nel suo celebre “Programma di Hilbert”, un ambizioso progetto volto a fondare tutta la matematica su basi assiomatiche sicure, dimostrandone la coerenza interna attraverso metodi finiti e costruttivi. Tuttavia, questa visione fu profondamente messa in crisi dai teoremi di incompletezza di Gödel nel 1931.

Oltre alla matematica, Hilbert contribuì in modo significativo anche alla fisica teorica. Collaborò con il fisico Albert Einstein allo sviluppo
delle equazioni della relatività generale, e lavorò sulla formulazione assiomatica della fisica.

Hilbert morì nel 1943, emarginato dal regime nazista a causa del suo sostegno agli scienziati ebrei. La sua eredità sopravvive in ogni angolo della matematica moderna. La sua celebre frase “Wir müssen wissen — wir werden wissen” (“Dobbiamo sapere — sapremo”) incarna il suo spirito razionale e il suo ottimismo.

Tuttavia, la sua capacità di unire rigore e creatività è forse illustrata al meglio dal paradosso dell’“Hotel Infinito”, che egli presentò durante
una conferenza pubblica negli anni ’20.

2. Il paradosso dell’Hotel Infinito

Immaginiamo un hotel con un numero infinito di stanze, numerate 1, 2, 3, 4 e così via, senza fine. Ogni stanza è occupata da un cliente.
A prima vista, sembrerebbe che non ci sia più spazio per nessuno. Tuttavia, essendo l’hotel infinito, Hilbert mostrò che si può sempre
trovare posto per nuovi arrivati, anche se l’hotel è completamente pieno.

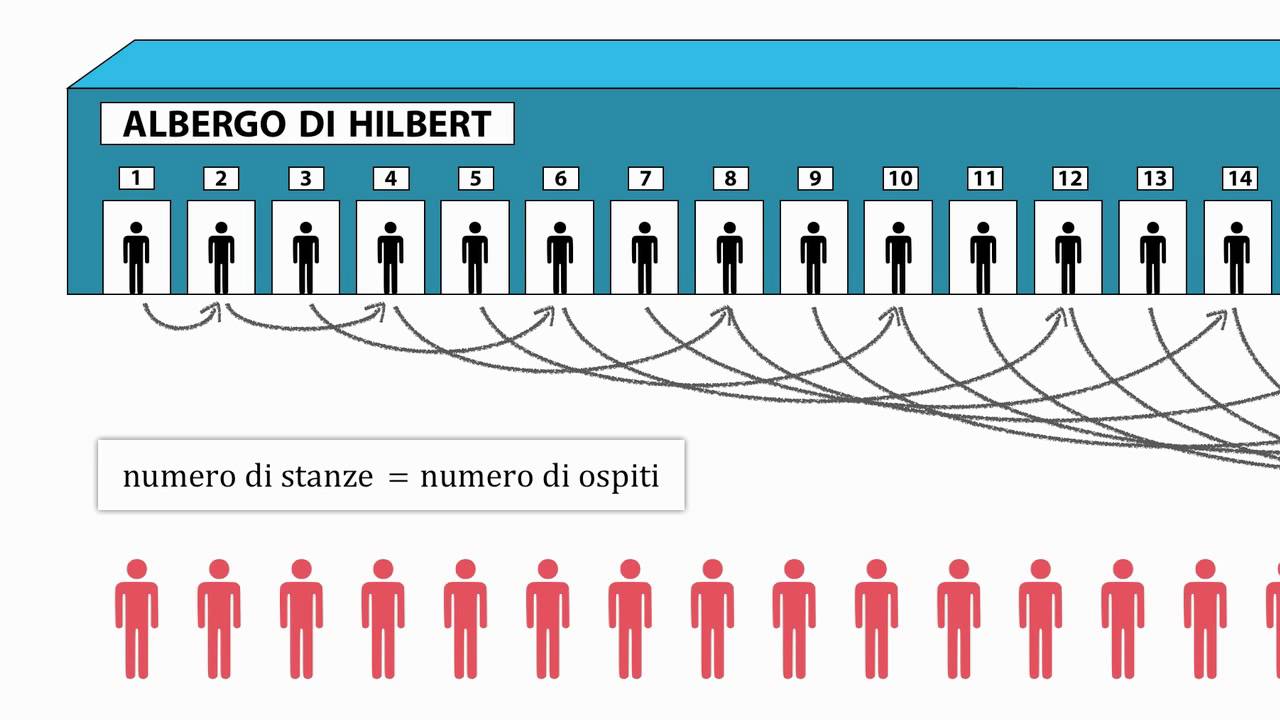
Caso 1: Arriva un nuovo cliente

Il direttore dell’hotel può semplicemente chiedere a ciascun ospite di spostarsi nella stanza successiva: l’ospite della stanza 1 va nella 2,
quello della 2 nella 3, e così via. Poiché il numero di stanze è infinito, nessuno resta senza sistemazione e la stanza 1 si libera per il nuovo cliente.

Caso 2: Arrivano infiniti nuovi clienti

Supponiamo ora che arrivi un numero infinito di nuovi clienti, anch’essi numerati 1, 2, 3, ecc. Anche in questo caso, l’hotel può accoglierli tutti. La strategia consiste nel chiedere agli ospiti attuali di spostarsi nella stanza con numero doppio rispetto a quello occupato (cioè, chi è nella stanza n va nella 2n). In questo modo, tutte le stanze dispari si liberano, lasciando infinite stanze disponibili per i nuovi arrivati.

Caso 3: Arriva un numero infinito di pullman con infiniti passeggeri ciascuno

Questo scenario più estremo prevede l’arrivo di infiniti autobus, ognuno con infiniti passeggeri. Anche qui, l’hotel può organizzare un sistema
di riassegnazione utilizzando tecniche della teoria degli insiemi (ad esempio, una funzione biiettiva tra N × N e N, come la numerazione
diagonale di Cantor), per sistemare tutti i nuovi ospiti.

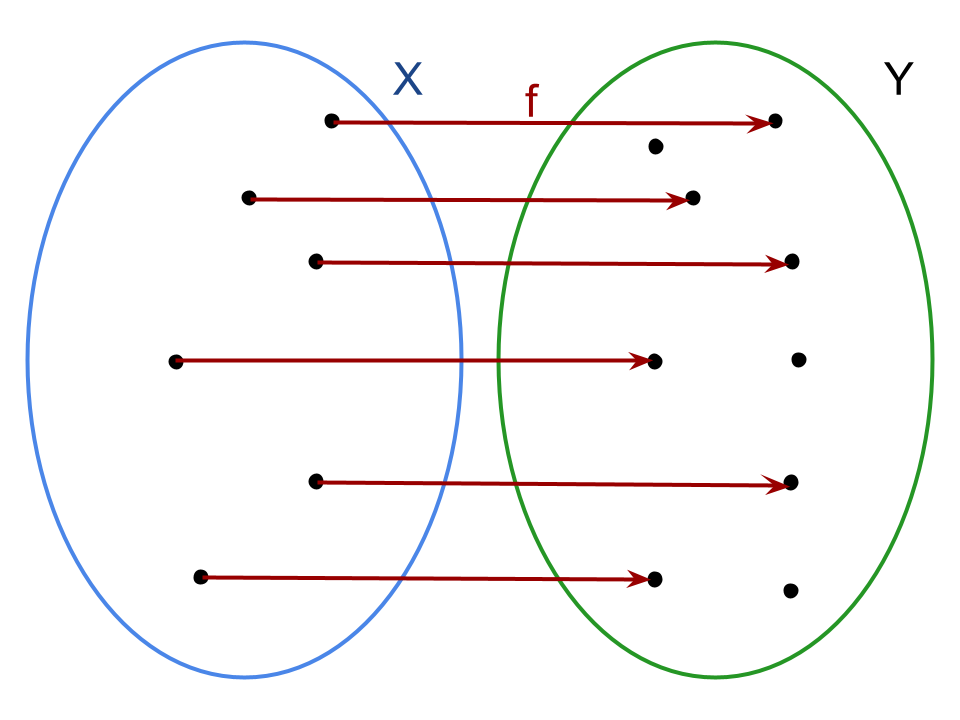
Rappresentazione grafica di una funzione biiettiva in cui per ogni valore x corrisponde un solo valore y

Caso 4: ospiti con nomi di infinite lettere casuali

Ora immaginiamo una nuova situazione. Arrivano infiniti nuovi ospiti, ma ciascuno di essi ha un nome infinito, una sequenza infinita di lettere scelte casualmente dall’alfabeto. Ad esempio:

• Alice diventa: AJIEZKALW… (infinita)
• Bob diventa: BDQKWELOM… (infinita)

Qui, ogni nome è una stringa infinita di caratteri, ad esempio lettere dell’alfabeto inglese (26 lettere). Matematicamente, ogni ospite è identificabile da un elemento della funzione:

f: N → A, dove A è l’alfabeto, e f è una funzione che assegna a ogni posizione n una lettera dell’alfabeto.

L’insieme di tutte queste funzioni è A^N (l’insieme delle sequenze infinite su A), ed è non numerabile. Infatti, ha la stessa cardinalità dell’insieme dei numeri reali — una cardinalità strettamente maggiore di quella dell’insieme dei numeri naturali.

Perché l’Hotel di Hilbert non può ospitarli?

L’Hotel di Hilbert ha un numero infinito numerabile di stanze: una per ciascun numero naturale. Tuttavia, i nuovi ospiti formano un insieme
non numerabile: l’insieme di tutte le stringhe infinite di lettere.

Ecco il punto cruciale: non esiste una corrispondenza biiettiva tra l’insieme dei numeri naturali e un insieme non numerabile.
Non importa quante strategie si adottino: se un insieme ha cardinalità maggiore di ℵ₀ (aleph-zero), non può essere mappato interamente in N, cioè non può essere sistemato in un hotel con stanze numerate da 1 a ∞.

Anche se l’hotel è “infinito”, non è abbastanza grande. Serve qualcosa di “più grande dell’infinito” numerabile: un’infinità non numerabile,
come quella dei numeri reali o delle sequenze infinite di lettere.

Questa estensione del paradosso di Hilbert ci mostra un punto fondamentale della teoria degli insiemi: non tutti gli infiniti sono uguali.
L’intuizione umana fatica a distinguere tra diversi “gradi di infinito”, ma la matematica, grazie a Cantor, ci insegna che alcuni infiniti sono
più grandi di altri.
L’Hotel di Hilbert può gestire tutti gli insiemi numerabili (come i naturali, gli interi, i razionali), ma fallisce quando si entra nel regno del
non numerabile, come i reali, le funzioni da N a un insieme finito, o le stringhe infinite di lettere.

Conclusione

L’Hotel di Hilbert è uno strumento straordinario per comprendere le proprietà paradossali dell’infinito. Ma il caso dei nomi infiniti ci mostra
i suoi limiti: ci porta dalla familiarità dell’infinito numerabile al mistero profondo dell’infinito non numerabile. Un viaggio che, pur partendo
da una semplice analogia, ci conduce ai confini della matematica e della logica, dove nemmeno un hotel infinito può bastare.